Wavelet Analysis

Scales

      In the previous section we saw how one can use a typical wavelet (the Morlet) to decompose a time series into time-frequency phase space. We now turn to the actual computation of the wavelet transform.

      The first thing to consider is the shape of the wavelet. For decomposing the NINO3 SST data, we chose the Morlet wavelet because:

  1. it is commonly used,
  2. it's simple,
  3. it looks like a wave.
There are an infinite number of other mother wavelets that could be chosen (see Farge 1992 for examples).

      For the Morlet wavelet transform, where the mother wavelet is:

Eqn 2.1

we must first choose the wavenumber w0, which gives the number of oscillations within the wavelet itself. One condition of the wavelet transform is that the average of the wavelet itself must be zero. In practice, if we choose w0=6, then the errors due to non-zero mean are smaller than the typical computer round-off errors (Farge 1992).

      Our next choice is a set of scaling parameters s, such that we adequately sample all the frequencies present in our time series. We first choose the smallest resolvable scale, s0, as some multiple of our time resolution, dt. For the NINO3 SST data, we have seasonal data, thus dt = 0.25 years. The smallest wavelet we could possibly resolve is 2dt, thus we choose s0 = 2dt = 0.5 years. The larger scales (longer periods) are chosen as power-of-two multiples of this smallest scale,

(3.1a) . . . . . . . . . .

(3.1b) . . . . . . . . . .

The largest scale chosen should be less than 1/2 the length of the entire time series. The choice of scales for the NINO3 SST data is shown on the right-hand axis of Figure 3. In theory, if these scales are chosen wisely, then one can construct an orthogonal complete basis set. In reality, one usually over-samples the scales so as to provide information on freqencies in between the orthogonal scales. Thus, in Figure 3, the scales have been over-sampled by choosing 10 sub-scales within each scale.

Algorithms

      It is possible to compute the wavelet transform in the time domain using Eqn 2.3. However, it is much simpler to use the fact that the wavelet transform is the convolution between the two functions x and Psi, and to carry out the wavelet transform in Fourier space using the Fast Fourier Transform (FFT). In the Fourier domain, the wavelet transform is simply,

(3.2) . . . . . . . . . .

where the ^ indicates the Fourier transform (FT), and the Fourier transform of the time series is given by:

(3.3) . . . . . . . . . .

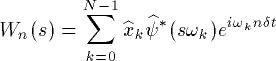
To use this formula, the FT of the wavelet function should be known analytically. In addition, the wavelets must be normalized as:

(3.4) . . . . . . . . . .

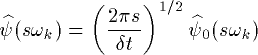
Unlike the convolution, the FFT method allows the computation of all n points simultaneously, and can be efficiently coded using any standard FFT package.

      The steps to compute the wavelet transform for a time series are thus:

  1. Choose a mother wavelet,
  2. Find the Fourier transform of the mother wavelet,
  3. Find the Fourier transform of the time series,
  4. Choose a minimum scale s0, and all other scales,
  5. For each scale, do:
  6. Make a contour plot.

      One problem with performing the wavelet transform in Fourier space is that this assumes the time series is periodic. The result is that signals in the wavelet transform at one end of the time series will get wrapped around to the other end. This effect is more pronouced at larger scales as the influence of each wavelet extends further in time. One way to avoid this is to pad one end of the time series with zeroes. A clever method is to pad with enough zeroes to make the length of the time series equal to a power of two, and thereby speed up the FFT as well.

-- on to Monte Carlo --

back to Wavelet Home Page